Wenn Sie Popcorn in die Mikrowelle geben, dann wird das im Maiskorn enthaltene Wasser durch die Hitze gasförmig und dehnt sich aus. Dadurch steigt der Druck im Inneren an, bis die feste Kornhülle platzt. Nun, dieses faszinierende Geheimnis haben wir für sie endlich gelüftet, aber was passiert eigentlich mit den Daten, die wir in unsere mathematische Mikrowelle geben, in der Hoffnung ebenfalls zuckersüße Resultate zu erzielen?
Denn neben der Qualität und der Validität der Datensätze, spielt auch die Herangehensweise und das passende Verfahren eine tragende Rolle für eine rechtliche Beurteilung bzw. Kontrollverfahren von Data Science Systemen (Verfahrensvalidität).
Die Hauptkomponentenanalyse, auch bekannt als PCA (Principal Component Analysis), gilt neben dem „Clustering“ und den „Association Rules“ zu den beliebtesten Verfahren, um Daten zu aggregieren und dadurch Trends zu erkennen.
WARNUNG. Auf eigene Gefahr.
Bitte halten Sie Aspirin und ein halbes Glas Wasser (Raumtemperatur) bereit. Dieser Artikel ist vermutlich nichts für schwache Nicht-Mathematik begeisterte Juristennerven.
Geschichtsstunde und Anwendung
Die Hauptkomponentenanalyse ist ein Verfahren in der sogenannten Unsupervised Methode (Unüberwachtes Lernen). Es ist eines der ältesten Ordinationsverfahren und wurde in der ersten Hälfte des 20. Jahrhunderts im angloamerikanischen Raum entwickelt. Seitdem dient dieses altbewehrte Urgestein unter den Verfahrensarten, zur Datenreduktion. Dabei werden beobachtete Variablen auf weniger nicht beobachtete Variablen reduziert. Die nicht beobachteten Variablen sind aus einem Bündel beobachteter Variablen zusammengesetzt und werden als „Hauptkomponenten“ oder auch „Faktoren“ bezeichnet.
Dieses Verfahren wird häufig zur Datenauswertung in der Psychologie, in den Naturwissenschaften, in der Chemie, in den Biowissenschaften, in der Medizin, in den Geowissenschaften, in den empirischen Sozialwissenschaften, aber auch im Marketingbereich verwendet.
Grundidee und Problemstellung
Angenommen wir wollen einen gemessenen Datensatz (X1, X2, …, Xn) visualisieren. Dabei steht jedes X für jeweils ein Merkmal.
Dann wäre es möglich bei nur wenigen Merkmalen ein zweidimensionales Diagramm (sog. Punktwolke) mit jeweils zwei Merkmalen graphisch darzustellen. Handelt es sich jedoch um eine größere Menge von Merkmalen, so wird die Anzahl der graphischen Darstellungen zu groß, um alle wichtigen Informationen auf den Diagrammen zu erkennen. Als Beispiel stellen wir uns einen Datensatz mit 8 Merkmalen vor, demnach
1 + 2 + 3 + 4 + 5 + 6 + 7 = p/2 = 28 Grafiken, welche insgesamt nicht mehr gut interpretierbar sind. Einige Grafiken enthalten wichtige Informationen, andere weniger wichtige Informationen, das bedeutet, dass alle Grafiken nur einen Bruchteil einer ganzen Information des Datensatzes enthalten.
Um dieses Problem zu begegnen wird nach einer niedrig-dimensionalen repräsentativen Darstellung, die den größten Teil der Informationen beinhaltet, gesucht. Damit könnte man im besten Fall eine zweidimensionale Darstellung des Datensatzes, die das Maximum aller Informationen beinhaltet, erzielen. Und genau das setzt die Hauptkomponentenanalyse (PCA) um. Die Hauptkomponentenanalyse findet eine niedrig-dimensionale repräsentative Darstellung des Datensatzes mit der größtmöglichen Streuung der Varianz, also dem größtmöglichen Informationsgehalt. Dahinter steht die Idee, dass nicht jede Beobachtung in einem n-dimensionalen Raum gleich wichtig ist. Die Hauptkomponentenanalyse sucht daher eine geringe Anzahl der Dimensionen, welches die wichtigsten Informationen größtmöglich beinhaltet. Die Information ist umso wichtiger, desto größer die Varianz ist. Jede Dimensionen wird durch die Hauptkomponentenanalyse gebildet und ist eine Linearkombination aller (n) Merkmale.
Für Nichtmathematiker ausgedrückt: Der übliche Umgang mit Prozessen erfolgt nach einem starren Stationsdurchlauf. Stellen Sie sich hierzu zunächst eine Fließbandfertigung von Autos vor. Als Arbeitsannahme stelle man sich hierzu 8 Stationen vor, die zu einem fertigen Auto führen (also vermutlich eher ein Tesla). Bisher mussten diese 8 Stationen durchlaufen werden, um ein bestimmtes Ziel zu erreichen. Diese 8 Stationen wurden immer gezielt gewählt, weil sie allein betrachtet wichtig sind. Betrachtet man jetzt aber die Kombination der 8 Stationen zusammen, so können sich neue Erkenntnisse bilden. Die neue Erkenntnis könnte sein, dass einige Stationen wichtiger sind, und andere, weniger bedeutsam, um an unser Ziel zu gelangen. Eine weitere Erkenntnis könnte auch sein, das eine Kombination der Stationen dazu führt, dass andere Stationen nicht oder kaum gebraucht werden. Zusammenfassend verändert man die Stationen so, um den optimalen Weg zum Ziel zu führen. Nach der Analyse könnten beispielsweise statt 8 Stationen nur noch 5 Stationskombinationen das Ziel erreichen und den Prozess schneller und effizienter gestalten.
Datenreduktion und Erkenntnisgewinn
Die Hauptkomponentenanalyse, als Datenreduktionsmethode, dient dazu die wichtigsten Informationen aus einem Datensatz zu bündeln und in Faktoren, oder einfach ausgedrückt in Gruppen, darzustellen. Ziel ist es aus dem vorhandenen Datenbestand neue Erkenntnisse zu erzielen und im besten Fall zu visualisieren. Um das zu gewährleisten, geht man in der Mathematik wie folgt vor:
In den Abbildungen 1 und 2 werden zweidimensionale Variablen in einem Raum (X1, X2) graphisch dargestellt. Bei dem Vorgang der Datenreduktion sucht man die optimale Trennung dieser Punkte, die sich im besten Fall in zwei plausible Gruppen trennen lassen. In Abbildung 1 sieht man die Punkte (X1, X2) eingezeichnet. Diese Punkte sind auf einer Geraden projiziert und mit einem blauen Kreis gekennzeichnet. Jedoch gibt es in dieser Form keine eindeutige Trennung der Punkte, da die Datenpunkte aufeinander liegen und nah beieinander sind. Die Varianz der Projektionsgeraden ist nicht maximal, sondern minimal. Wir suchen aber eine Gerade, in der die Varianz maximal ist, damit man die Datenpunkte besser auseinander halten kann, um so erst eine aggregierte Darstellung vorzunehmen.
In Abbildung 2 ist so eine Gerade zu finden und auch eingezeichnet worden. Diese Gerade enthält die Richtung mit der größten Veränderung der Daten, um die Trennung in den zwei Gruppen besser zu erkennen.
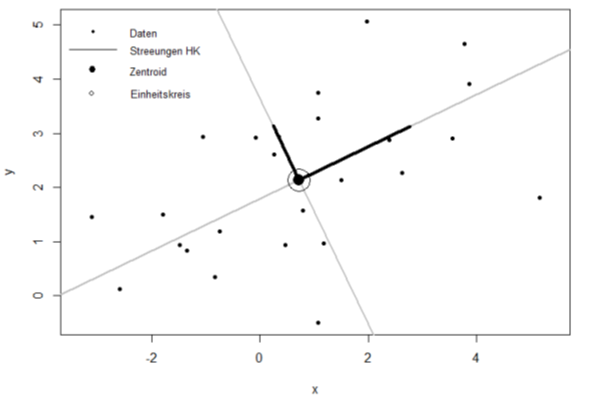
Abbildung 1: Projektionsgerade in Richtung minimaler Varianz der Daten. (PC2 – Hauptkomponente 2)
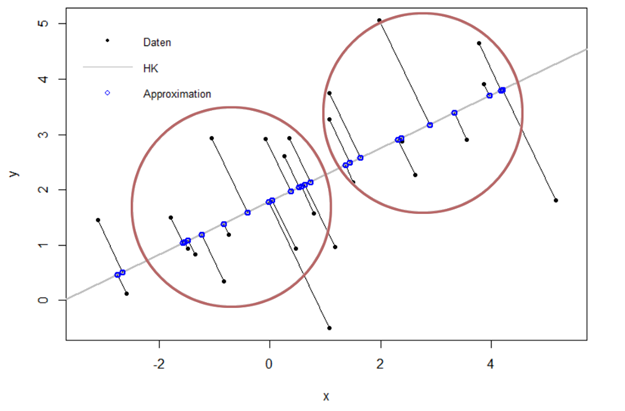
Abbildung 2: Projektionsgerade in Richtung maximaler Varianz der Daten. (PC1 – Hauptkomponente 1)
Hierdurch werden die zweidimensionalen Daten in einem eindimensionalen Raum dargestellt. Diesen Vorgang nennt man Datenreduktion. Das ist auch unsere erste Hauptkomponente (PC1 genannt). Damit haben wir die wichtigsten Informationen auf diese erste Hauptkomponente reduziert und somit die größtmögliche Varianz erzielt. Die zweite Hauptkomponente (PC2) aus Abbildung 1 umfasst die nächstgrößere Varianz, die nicht mit der ersten Hauptkomponente korreliert, das heißt die Gerade liegt orthogonal (senkrecht) auf der ersten Hauptkomponente. Die Korrelation beschreibt die Abhängigkeit zwischen den beiden Hauptkomponenten PC1 (Abbildung 2) und PC2 (Abbildung 1). Einfach ausgedrückt, die Informationen in PC1 und PC2 überschneiden sich nicht und sind vollkommen unabhängig voneinander. PC2 ist hier überflüssig für den Informationsgehalt, denn PC1 allein teilt die zwei Gruppen (rot eingezeichnet) ein. Somit haben wir eine Datenreduktion mit PC1 erreicht. Statt zwei Geraden wird jetzt nur noch PC1 (eine Gerade) betrachtet, um die wichtigen Informationen zu erkennen.
Für Nichtmathematiker ausgedrückt: Um sich das besser vorzustellen, nehmen Sie 8 verschiedene Charaktereigenschaften, welche bei einigen Probanden gewisse Zusammenhänge aufweisen. Die Hauptkomponentenanalyse (PCA) zieht mithilfe der ersten Hauptkomponente (PC1) diejenigen Eigenschaft raus, welche die stärksten Zusammenhänge aufweist (bspw. aggressiv, impulsiv, wütend, cholerisch etc.). Die zweite Hauptkomponente (PC2), weist hingegen die zweitstärksten Zusammenhänge auf (bspw. freundlich, glücklich, tolerant, liebevoll), die mit der PC1 keine Berührungspunkte hat. Hierdurch werden die 8 Charaktereigenschaften des Probanden auf 2 Hauptkomponente reduziert (siehe unten genauer).
Um mit den Daten sinnvolle Rechnungen anzustellen werden die Hauptkomponenten anschließend in einem neuen Koordinatensystems mit neuen Hauptachsen dargestellt. Diese Achsentransformationen ist von Abbildung 3 auf Abbildung 4 zu erkennen. Der Ursprung des neuen Koordinatensystems bestimmt den Schwerpunkt (Zentroid) aller Daten, der durch den Mittelwert jeder Variable berechnet wird. Dadurch soll erreicht werden, dass die Daten besser interpretierbar sind. Diesen Vorgang bezeichnet man in der Linearen Algebra als Basistransformation.

Abbildung 3: Ursprüngliches Hauptachsenkoordinatensystem
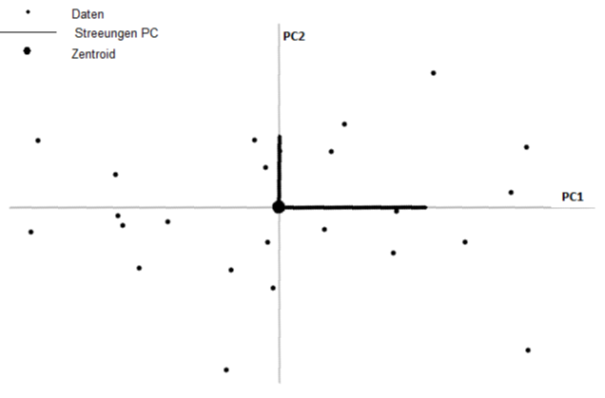
Abbildung 4: Neues Hauptachsenkoordinatensystem
Ein Beispiel
Für die Durchführung der Hauptkomponentenanalyse wird ein Datensatz mit psychologischen Daten verwendet. In diesem Datensatz sind 4 verschiedene Adjektive enthalten die Persönlichkeitsmerkmale bzw. Eigenschaften von 10 Probanden beschreiben. Dabei sind die Persönlichkeitsmerkmale folgende:
| Angriffslustig | Streitbar |
| Kleinlich | Übergenau |
Jeder Proband gibt für jedes Merkmal eine Einschätzung über sich selbst in einer Skala 1-10 ab. Dabei repräsentiert der Wert 1 einen nicht zutreffendes Persönlichkeitsmerkmal und der Wert 10 einen absolut zutreffendes Persönlichkeitsmerkmal. Bei diesen Merkmalen handelt es sich um quantitative Merkmale. Zunächst wird die Tabelle aufgestellt:
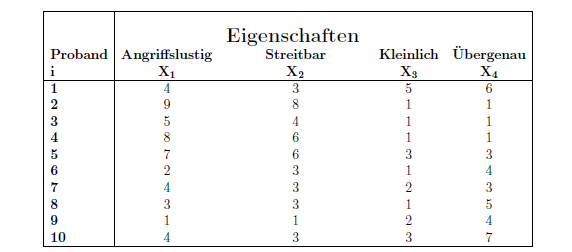
Die Ausgangsdatenmatrix wird betrachtet, um einen ersten Eindruck zu erhalten. Man könnte auf den ersten Blick meinen, dass die Eigenschaften „Angriffslustig“ und „Streitbar“ große Werte besitzen, wenn die jeweils andere Eigenschaft einen großen Wert hat.
Erkennbar ist auch, dass die Eigenschaften „Kleinlich“ und “ Übergenau“ eher kleine Werte haben, wenn die Eigenschaften „Angriffslustig“ und „Streitbar“ größere Werte annehmen. Die Tendenz der zwei Gruppen (X1, X2) und (X3, X4) sind mit bloßem Auge zu erkennen.
Die Grundüberlegung ist, die vier bestehenden Dimensionen auf zwei Dimensionen zu reduzieren. Die Gruppen (X1, X2) und (X3, X4) könnten jeweils zu einer Hauptkomponente gebündelt werden.
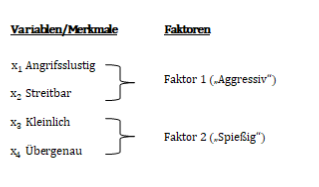
Somit würde Faktor 1 die Variablen (X1, X2) bündeln, diese Variablen beschreiben ein aggressives Verhalten, deswegen nennen wir diesen Faktor „Aggressiv“. Faktor 2 bekommt die Bezeichnung „Spießig“.
Dies muss nun mathematisch belegt werden.
Wir ersparen Ihnen jedoch die einzelnen Schritte, da Sie sich sonst mit folgenden Formeln auseinandersetzen müssten:
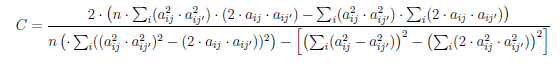
Wenn Sie nach dieser Formel noch nicht den Bildschirm ausgeschaltet haben und weggerannt sind und zusätzlich verstehen möchten was alles beachtet werden muss, um diese Formel zu verstehen, dann schicken Sie uns gerne eine Rückmeldung. 😀

Ein Jurist mit einem Faible für die Verzahnung von IT und Recht.
Und eine Mathematikerin die auch mit Zahlen umgehen kann.

